When can a connection be classified as shear? At its core, it is a junction that is designed to bear shear forces without any bending moment. While this description generally holds in theory, pure shear is an idealisation and there are instances where a bending moment accompanies the shear force in the connection. This is a crucial factor or aspect for structural engineers to consider when determining the connection`s design.
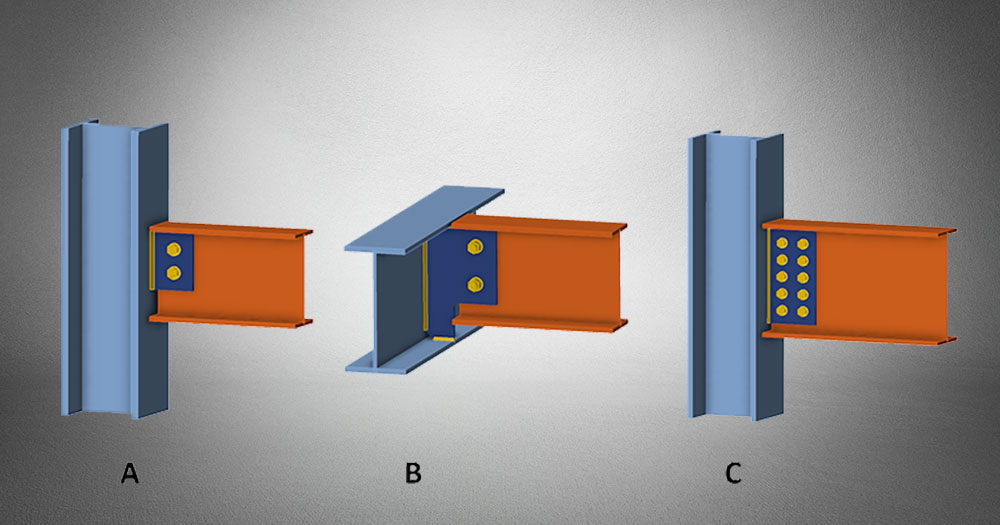
The article will illustrate three common methods of attaching an I-beam using a vertical connection plate (a fin plate) to either a column or a support beam. This setup is also referred to as a single plate shear connection. Each of these connections results in different behaviours when transferring loads.
Connection A
Connection A – Simple Shear Connection
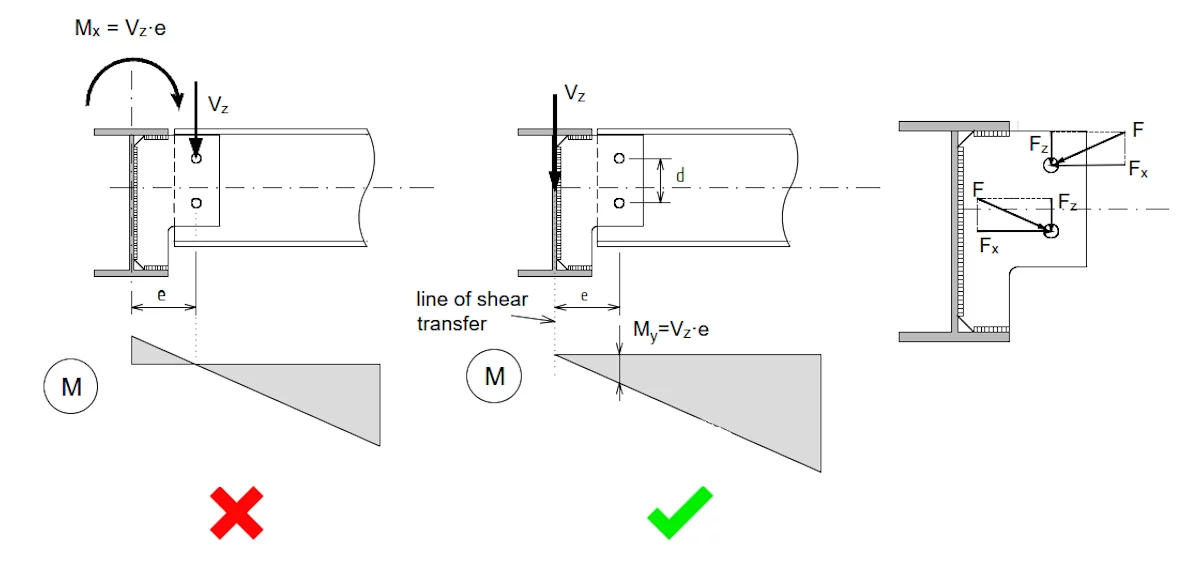
Connection A illustrates a basic shear connection, where a horizontal beam is attached to a column using a fin plate secured with a single column of bolts. Due to this configuration, the connection`s ability to resist rotation is very limited. Moreover, design practice typically accounts for the tolerance at the bolt holes by treating the connections as if they are pinned at the bolt grid. The distribution of the bending moments on the connecting beam is illustrated in connection A, demonstrating that the bending moment at the bolts is zero, corresponding to the hinge position, with the bolts bearing only the vertical force (Vz). This leads to a shear of the same magnitude alongside a bending moment (M), which is the product of Vz and the eccentricity (e); (M=Vz*e) at the weld position.
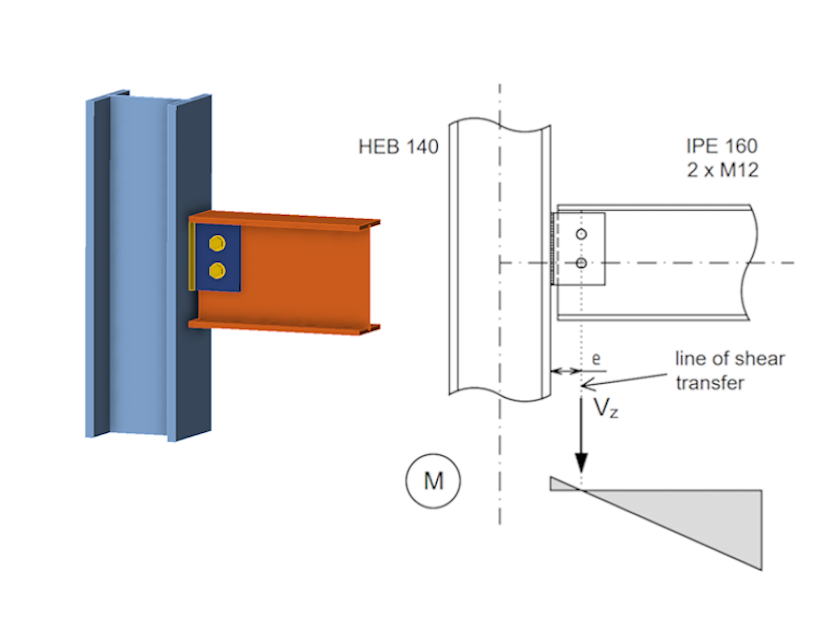
Connection A – Load Position
In the IDEA StatiCa Connection application, if this hinge position is assumed then this can be defined with ease by inputting the vertical shear force and setting the load position at the centre of the bolts.

Connection B
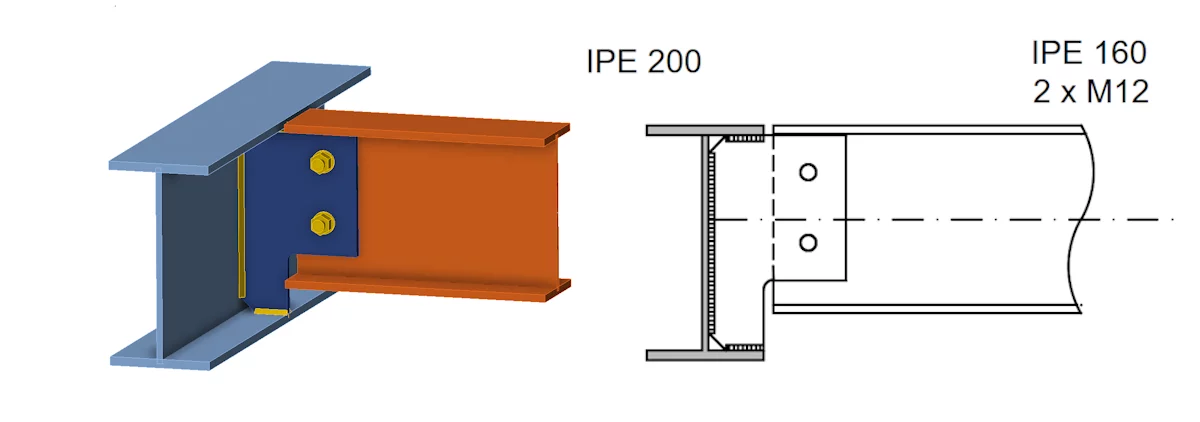
Connection B – Shear Connection
Connection B, another variant of shear connection, is instead used to support a secondary beam (i.e. beam – beam fin plate).
Shear force analysis diagram
If the hinge position is assumed to be similar to that in connection A, then this would lead to a torsional moment at the weld location, which in this case is an open section.
In reality, due to the (generally) very low torsional stiffness of open sections, the hinge would instead be often at the supporting beam web, with a moment developing at the bolt location. The force acting on each bolt is due to both vertical components (Fz = Vz/2) and horizontal components (moment couple, Fx = M/d).
How is this modelled in IDEA StatiCa?
When using the connection application, this type of response and loading can be defined with ease by entering only the vertical shear force and leaving the load position at the Node (default), assuming the supporting beam web coincides with it.
However, if the torsional stiffness of the supporting beam is not negligible, then this should be accounted for in the applied moment. In these cases, this would mean shifting the hinge along the supported member axis; the resulting hinge would be somewhere between the weld and the bolt grid.
So, when will this occur? Obviously when a torsionally rigid section of the girder is used, but also for connections that are positioned close to locations where the girder is supported (for example, the ends). In other words, on a girder that supports a series of secondary beams, we can have shear connections that correspond in behaviour to both connection A (near the supports) and connection B (midspan of the girder).

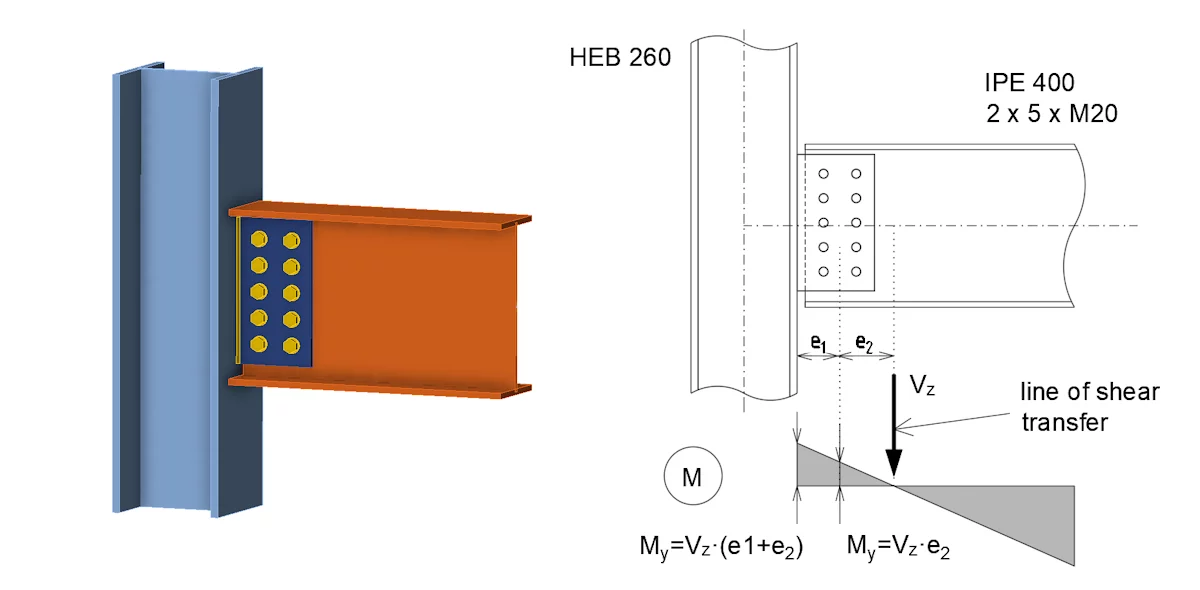
Connection C
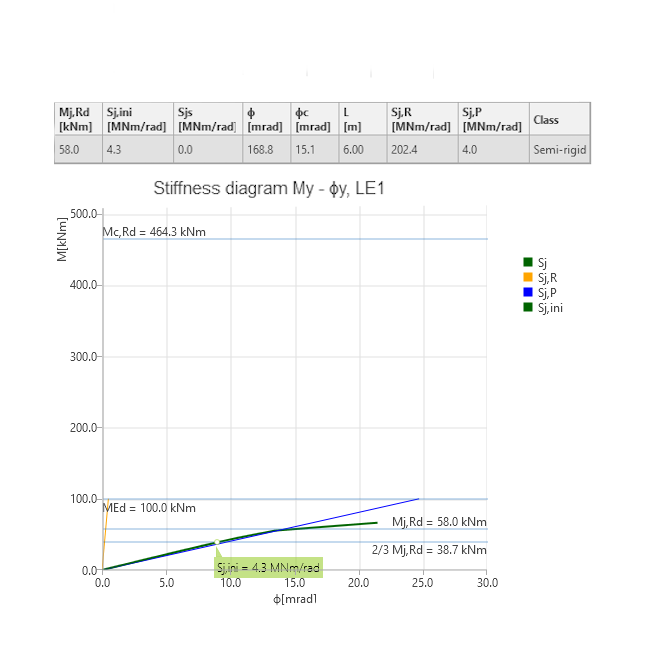
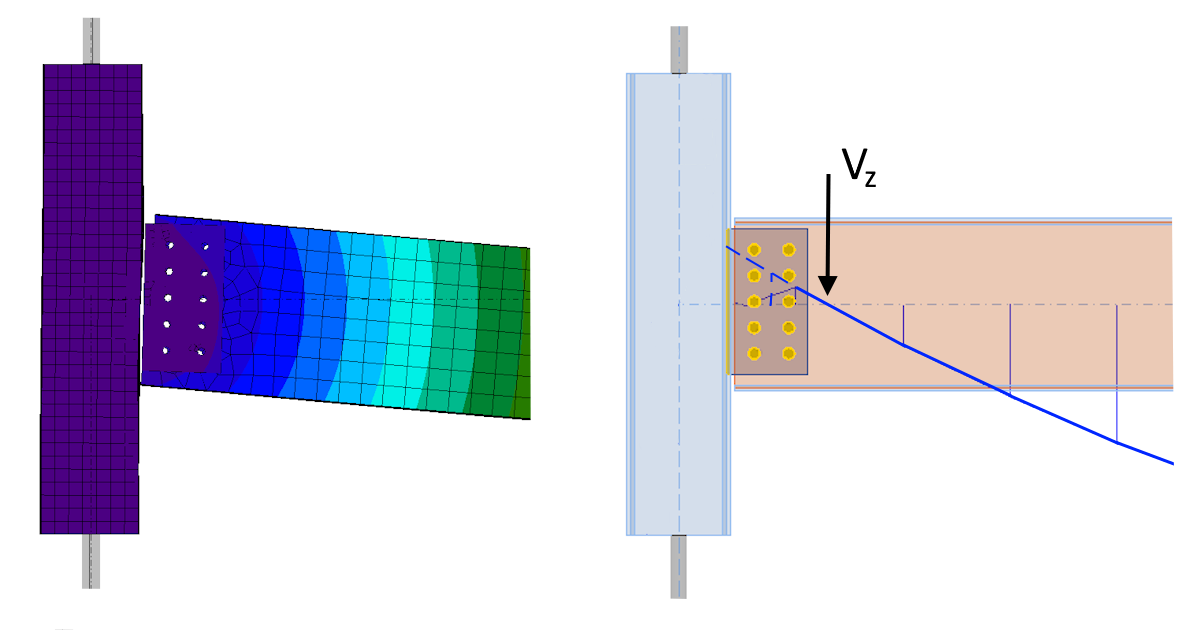
In connection C, there is a “large” single plate shear beam – column connection. In this case, consider that there are 10 bolts arranged in 5 rows of 2 bolts each at the fin plate, resulting in the connection having a considerable rotational stiffness, which, as a result, would affect the distribution of internal forces. This position of the zero bending moment will shift towards the midspan of the connection beam and a negative bending moment (M=Vz.e2) will be applied at the centre of the bolt group. The magnitude of the moment (or the magnitude of the eccentricity, e2 ) will depend on the rotational stiffness of the bolted connection. The stiffness can be calculated using IDEA StatiCa Connection’s Stiffness (ST) analysis, and then the calculated stiffness of the connection can be categorised according to the design code.
If the connection is categorised as pinned and has sufficient rotational capacity, the simplification of the small amount of bending force transmitted through the connection can be ignored. The allocation of internal forces within the connection can then be examined in a similar way to connection A. However, if the engineer decides to ignore the simplification or the connection is labelled as partially flexible, the determined rotational rigidity of the connection must be incorporated into the overall analysis model. The bending force within the connection is then computed and the connection is assessed for shear and moment, using the IDEA StatiCa Connection application.
Analysis with IDEA StaticCa Member
One may argue that the described behaviour of shear connection is only a hypothesis, so accompanying calculations can be used to confirm the outlined behaviour. This is where IDEA StatiCa Member comes in, as we can use the application to verify the behaviour of the shear connection numerically. IDEA StatiCa Member allows us to model the behaviour of steel structures, or their parts, to a high level of accuracy. Moreover, the individual members are modelled in 3D, using shell elements as part of a Component-based Finite Element Method (CBFEM) model.
This means that the individual components of the connections, for example, bolts, connection plate welds, etc, are directly included in the 3D computational model. The stiffness distribution and spatial behaviour of the structure are thus realistically represented in the mathematical model. IDEA StatiCa Member allows us to display internal forces in an individual member, which are then calculated by backward integration of the stresses from the shell elements.
Let’s compare the bending moment diagrams at the connections calculated by the Member app with the diagrams presented above for individual connections.
Connection A analysed by IDEA StatiCa Member:
First, let`s look at connection A. The image above illustrates a simple structure consisting of a pair of columns defined using HEB140 sections. An IPE160 section is connected to the columns by connection A. The length of the beam is 4m and the load is 10 kN/m. The bending moment diagram is illustrated in the following figure. There is close to zero bending moment at the bolted connection point and the moment shape corresponds very well to what was presented in the analysis of connection A`s response.
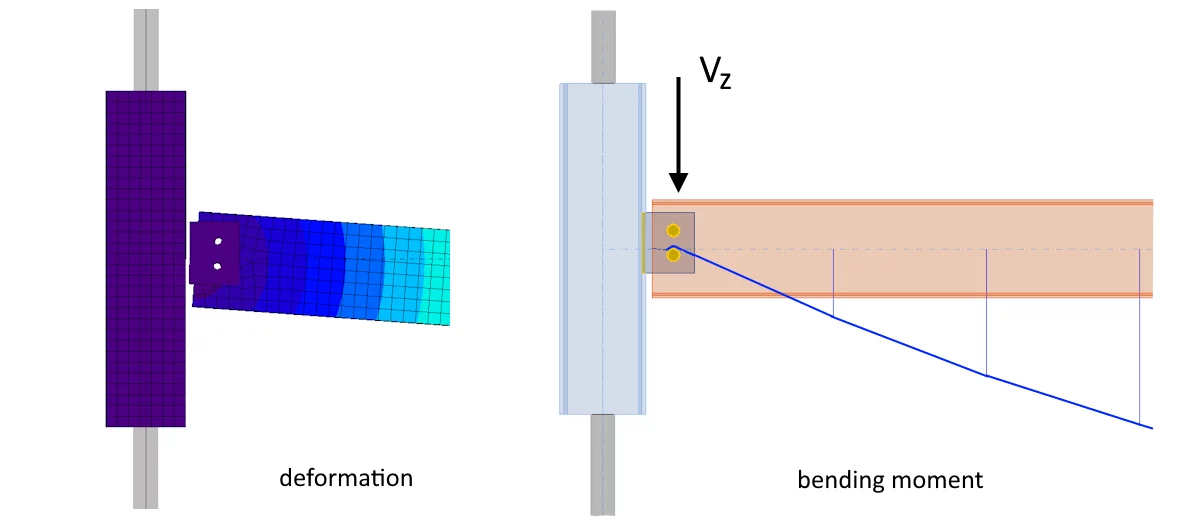

Connection B analysed by IDEA StatiCa Member:
Let us now verify the response of Connection B on a simple structure consisting of a pair of IPE200 girders of four meters in length. The flanges are simply-supported at the ends and torsionally fixed. A beam using an IPE160 section is supported by the main beams using Connection B. Once again, the load is 10 kN/m. Therefore, the bending moments on the beam are not displayed up to the axis of the girder and the extrapolated moment curve is represented with a dashed line. There is a positive bending moment at the position of the bolts and extrapolated with the moment curve has a near-zero value at the wall of the girder. Therefore, the moment diagram and the point vertical force, (Vz ) again correspond very well to what was presented in the analysis of the response of the type B connection.

So, what are the forces in the individual bolts in the connection? The vertical shear force in the beam leads to a bolt shear of 10 kN. for each of the bolts. The total shear force in a bolt (from the vertical shear force and moment in the connection) in this case is 31 kN. This response is three times higher value compared to the response of the type A connections. Please take into consideration that this example would not be universally true. This is because shear force also depends on the dimensions of the beams, the distance of the bolts from the girder wall, etc. However, it can seen designing a type B connection, and disregarding the moment can be considered to be a fatal mistake.

Let`s look at the situation discussed before, where the connected I-beam is moved to 0.5 m. from the support.
According to the earlier analysis, the bending moment should be changed because the amount the girder to twist is restricted at the supports. Moreover, the forces’ distribution should be positioned close to the response of the type A connection. In this instance, the zero moment is almost at the centre of the bolts group and the bolts are loaded by the vertical shear force.

Connection C analysed by IDEA StatiCa Member:
We will again use a simple construction consisting of a pair of a columns made from HEB240 profiles and a beam made of an IPE400 profile, which is connected to the columns using the C-type shear connection. The length of the beam is 6 m. and the load is 80 kN/m.

The bending moment diagram is illustrated in the following figure. There is a negative bending moment at the centre of the bolt group (again illustrated by extrapolating the moment on the beam). The connection thus behaves as a semi-rigid one. This is also confirmed by the stiffness analysis and categorisation of the connection in the Connection app.