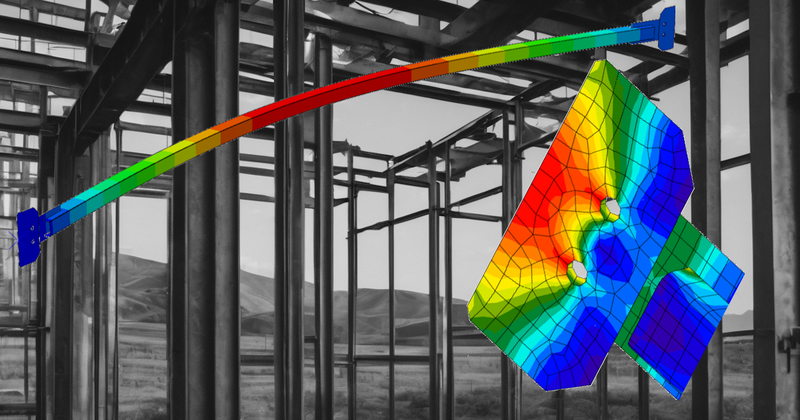
IDEA StatiCA Design & ABAQUS Verifying via HESCO.
The importance of Longitudinal Bracing in steel hall structures is paramount. It provides essential stability and structural integrity by countering lateral loads and preventing buckling. Discover how to efficiently, quickly, and safely design such a member using IDEA StatiCa Member and then conduct verification with ABAQUS through the projects led by HESCO.
HESCO led the project, with engineer Luciák Lesnak at the helm, skillfully designing and overseeing the code check for the hall. This impressive structure stretched 8.3 meters wide and a length of 22.6 meters long, with a height of 2.3 meters. A notable challenge in the hall’s development was working with the SHS profile, which was 50x50x3 mm in size. This piece was carefully welded onto an IPE 180, using an eccentric gusset plate, a task that required meticulous attention and analysis.
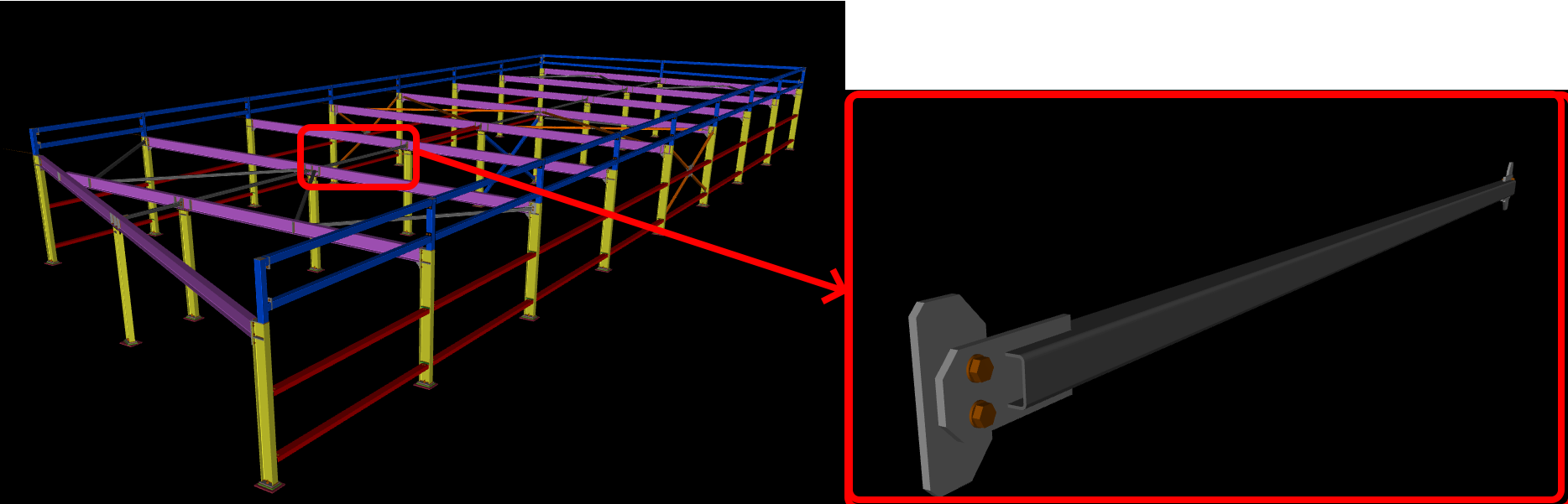
IDEA StatiCa Approach for Analytical solution
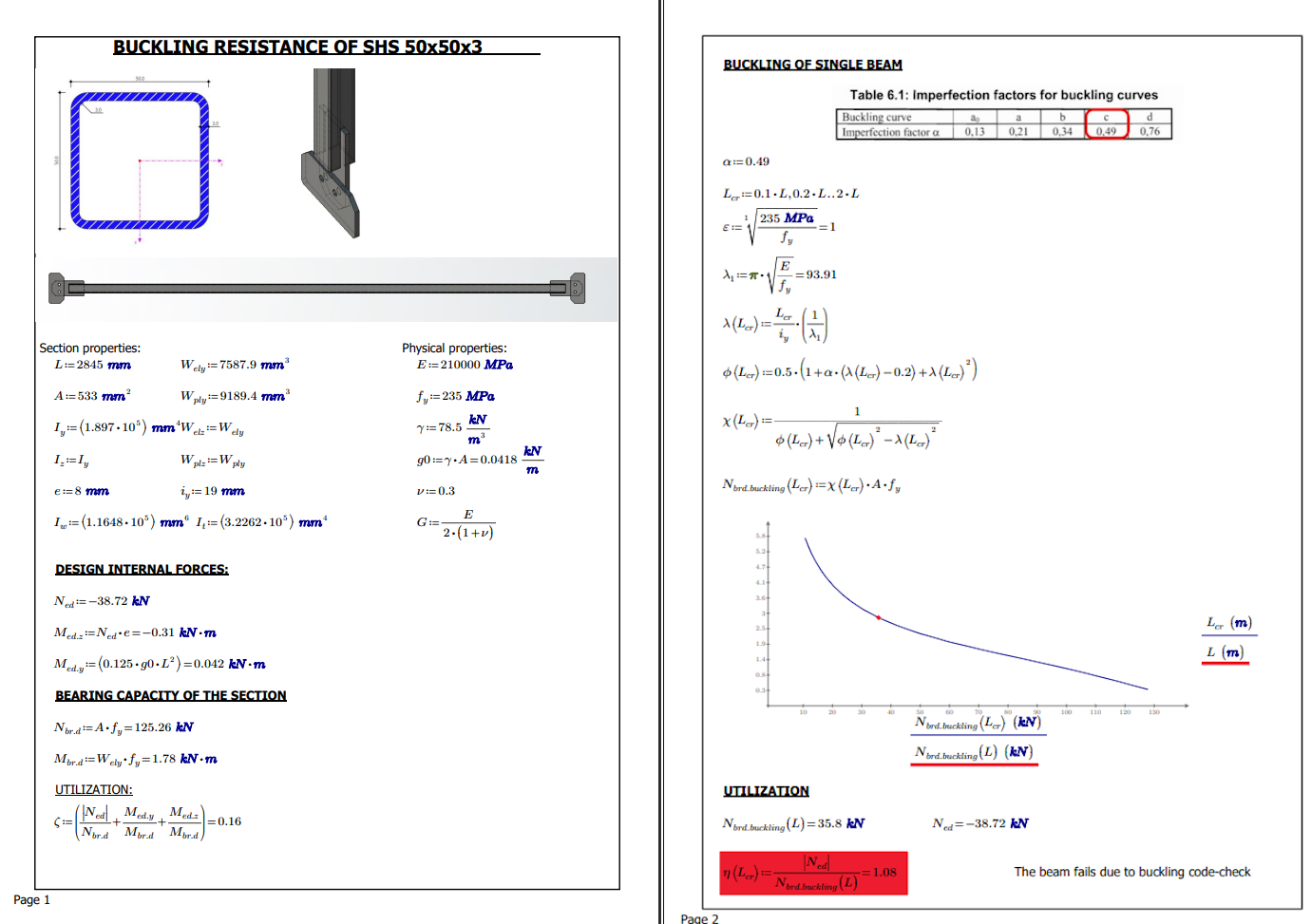
To carry out an advanced analysis of the HESCO project, it is important to hand-calculate and become familiar with a critical member`s behaviour. The hand calculation is performed using EN-1993-1-1. This calculation considers the design axial force and code checks for critical axial buckling resistance.
The benefits of hand calculations:
Understanding of principles: Allows engineers to gain a deep understanding of the fundamental principles and theories behind structural analysis and design. It helps them develop a strong foundation of knowledge and problem-solving skills.
Verification and validation: Serve as a valuable tool for verifying and validating the results obtained from computer-based analysis and design software. By performing independent calculations, engineers can ensure the accuracy and reliability of their designs.
Sensitivity analysis: Enables engineers to perform sensitivity analysis by manually adjusting various design parameters and observing their impact on the overall structural behavior. This helps in optimizing the design and identifying critical factors affecting structural performance.
Quick estimations: Provides a quick and efficient way to estimate structural responses and check the feasibility of preliminary design concepts. They can be performed during the early stages of a project when detailed computer-based analysis may not be necessary.
Enhanced problem-solving skills: Engineers can develop strong problem-solving skills and critical thinking abilities. They learn to break down complex structural problems into simpler components, analyze them systematically, and arrive at accurate solutions.
Educational purposes: Used as teaching tools in structural engineering education. They help students grasp the underlying concepts, theories, and equations involved in structural analysis and design, fostering a deeper understanding of the subject matter.
The imperfections of hand calculations:
Human error: The accuracy of hand calculations is highly dependent on the engineers’ skills, experience, and attention to detail. Errors in data entry, unit conversions, or mathematical calculations can lead to incorrect results, compromising the safety and reliability of the structure.
Limited complexity: Hand calculations are typically limited to simple structural systems. As the complexity of the structure increases, so does the complexity of the calculations, making it more challenging to perform them accurately and reliably.
Time-consuming: Hand calculations can be time-consuming and labor-intensive, particularly for large and complex structures. This can lead to delays in project timelines and increased project costs.
Limited optimization: Hand calculations are unsuited for optimization and iterative design processes. They are typically performed after the preliminary design has been established, limiting the ability to explore and optimize different design options.
Limited visualization: Hand calculations provide limited visualization of the structural behavior, making it challenging to identify potential failure modes or visualize the overall structural response.
While hand calculations offer several benefits, they are not without limitations and imperfections. It is essential to balance the advantages and disadvantages of hand calculations with other analysis tools and techniques to ensure accurate and reliable structural designs.
Numerical simulation for HESCO Project
For the HESCO project, the structural engineering team rigorously cross-checked the IDEA Statica Member model against results from ABAQUS to guarantee its robustness and reliability. This step was crucial in establishing a solid base for the structural design. Their in-depth analysis enabled the engineers to pinpoint any areas needing enhancement. This allows for precise adjustments to the model in the HESCO project. This thorough verification not only improved the model’s accuracy but also significantly uplifted the quality and safety of the overall structural design.
IDEA StatiCa and ABAQUS: Assumptions
The simulation of the numerical twin in ABAQUS incorporates specific assumptions for accuracy in HESCO project. The S4R element, a standard linear quad element known for reduced integration, hourglass control, and finite membrane strains, was chosen for modeling. To accurately represent bolts, a combination of join + revolute MPC and kinematic coupling was used in the HESCO project, ensuring stress distribution is correctly modeled in the nut and bolt head areas. Considering the presence of butt welds in the model, linear constraint ties were employed to effectively bind the plates.
The material properties in the simulation mirror those in the IDEA StatiCa model, ensuring consistency. Contacts within the model are set to be frictionless for the HESCO Project. A general static analysis complemented by a large displacement analysis was conducted to assess the model’s performance. The meshing is finely tuned, with a maximum size of 2 mm in connection areas and a 5 mm mesh size for the SHS 50/50/3.
Additional elements of the simulation include:
– Shell finite elements for structural integrity.
– Bolts modeled as nonlinear springs to account for interaction in tension and shear.
– Special elements for welds, bonding the plates via MPC for a more accurate representation.
– Frictionless contacts implemented using the penalty method.
– Material properties defined by a bilinear diagram with hardening, following an isotropic rule.
– Linear buckling analysis, with material nonlinear analysis serving as the preload and contacts free during the analysis for a realistic evaluation of structural behavior.
You can read the theoretical background here.
IDEA StatiCa and ABAQUS Analytical model
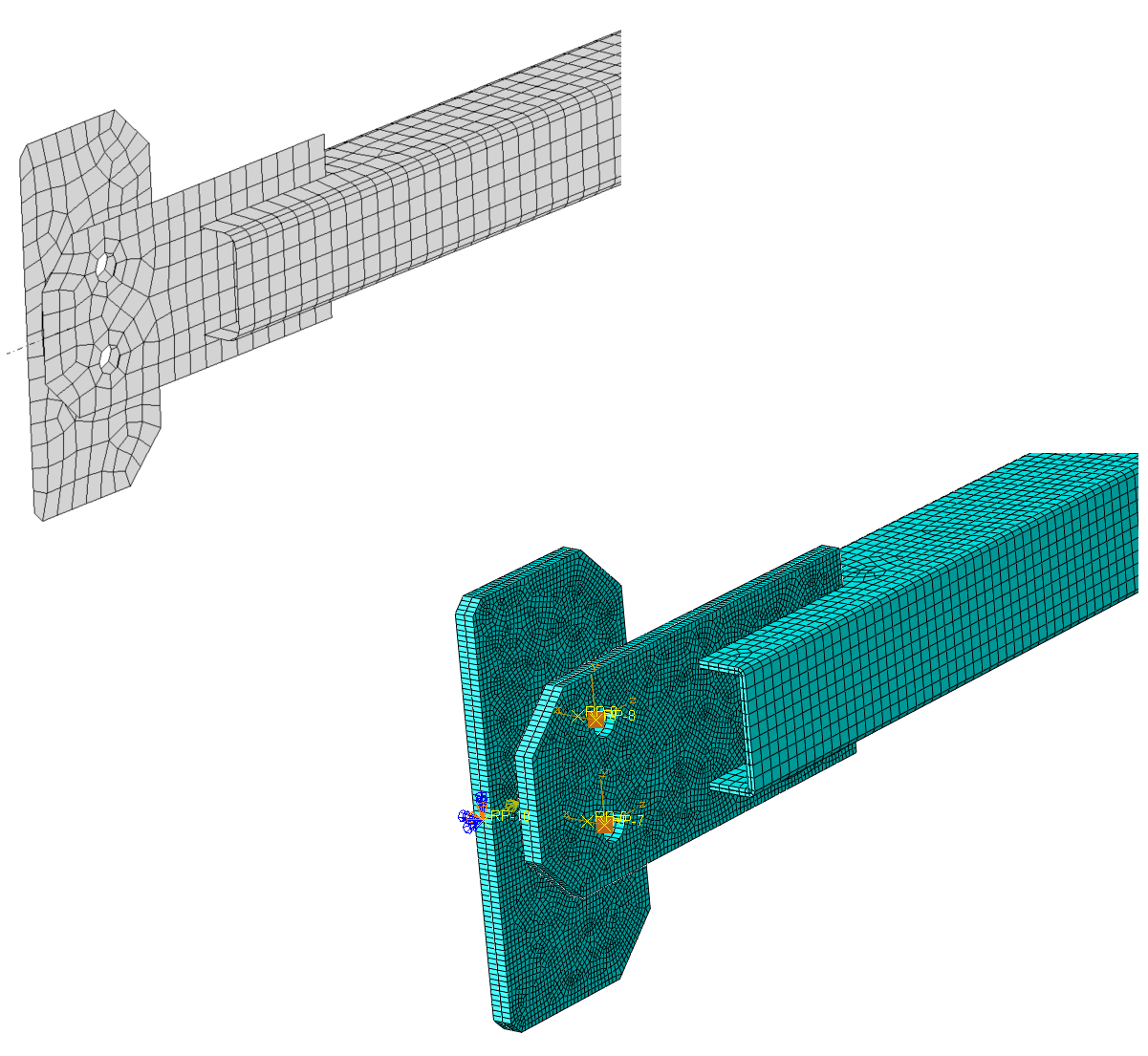
In the setup of our analytical model in the HESCO project, we’ve carefully controlled how it can move and rotate. We locked down one part of the model completely – it can’t twist, turn, or slide in any direction. But for the second part, we did something different: we let it slide along the axis of the SHS member, which is like a hollow square tube. We did this because we needed to see how the model handles the straight pushing and pulling forces that act right along that tube. It’s a way to make sure our model acts like it would in real life, under those specific conditions.
01) IDEA StatiCa model(left), ABAQUS model(right)
IDEA StatiCa and ABAQUS: Mesh Solution

In the IDEA StatiCa solution, we used the default mesh size, while for ABAQUS, we opted for a mesh size ranging from 2 to 5 mm.
02) IDEA StatiCa mesh(left), ABAQUS mesh(right)
IDEA StatiCa and ABAQUS: Load Solution
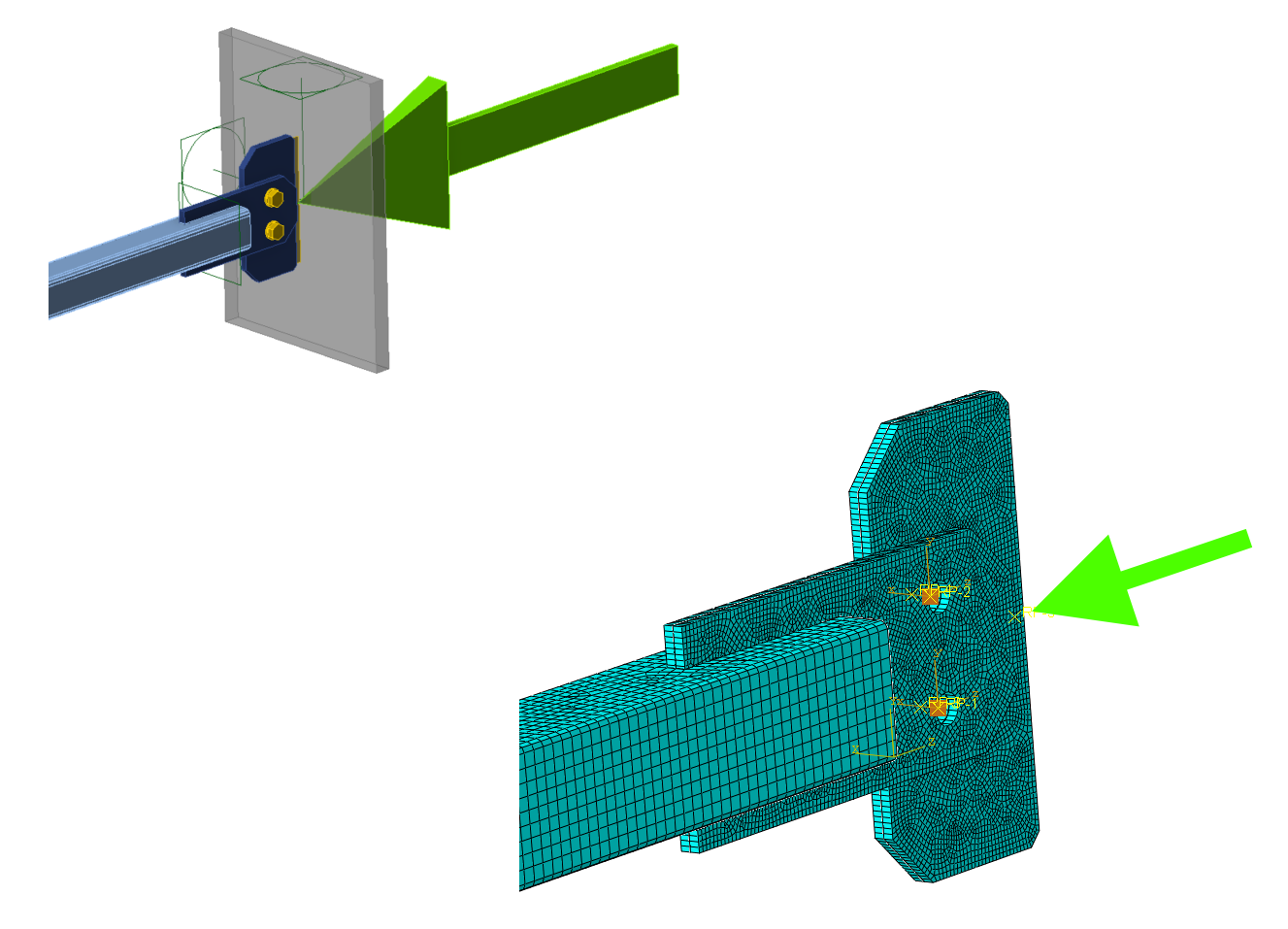
03) IDEA StatiCa load(left), ABAQUS load(right)
Geometrical and material nonlinear analysis
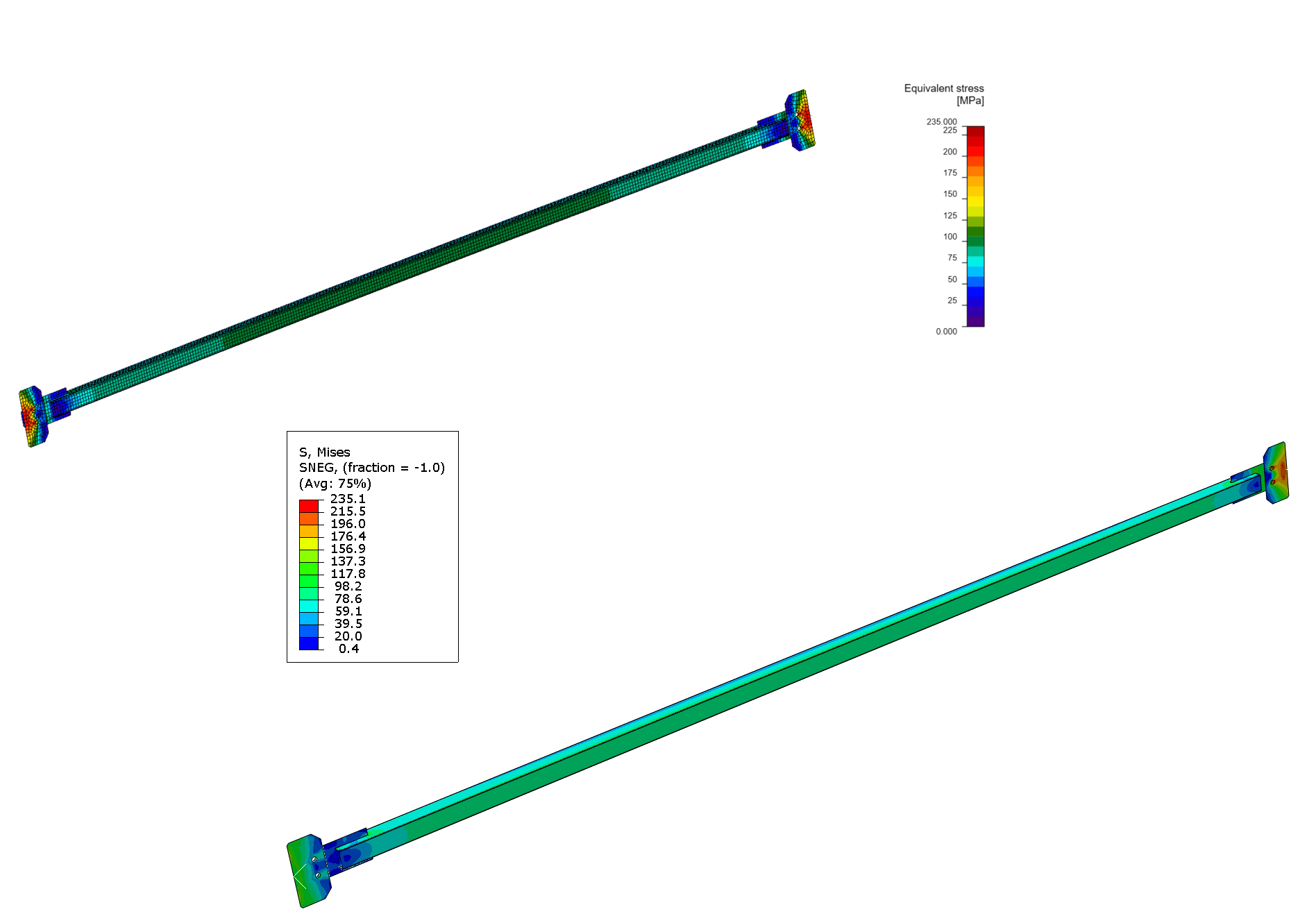
04) IDEA StatiCa equivalent stress(left), ABAQUS equivalent stress(right)
Geometrical and material nonlinear analysis is a powerful method used to understand how structures behave under large deformations and complex material responses. It dives into how the shape and material of a structure interact under extreme conditions, like when a material bends a lot or changes shape permanently.
The main goal here is to figure out how much stress and movement the structure can handle. We use the Newton-Rhapson method in each step to make sure the structure stays balanced even as it bends or stretches. This method takes into account all the tricky parts, like how the materials behave and how different parts of the structure touch and affect each other.
One important thing we look at is the equivalent stress, which tells us how the stress is spreading out across the structure. What’s interesting is that in both models we looked at, the way stress was distributed turned out to be pretty similar, showing that our approach is consistent and reliable in different scenarios.
IDEA StatiCA Other resources to hollow section connections
The HSS connection design and analysis couldn’t be precise enough without the GMNA (geometrically and materially nonlinear analysis). What was it developed for and when to use it? All the necessary information is summed up in one of the previous blog posts dedicated to this topic.
If you’re looking for some inspiration for circular hollow sections, you could be interested in these webinars dedicated to CHS bracing member connection and to 3D multimember connection combining CHS and SHS profiles.
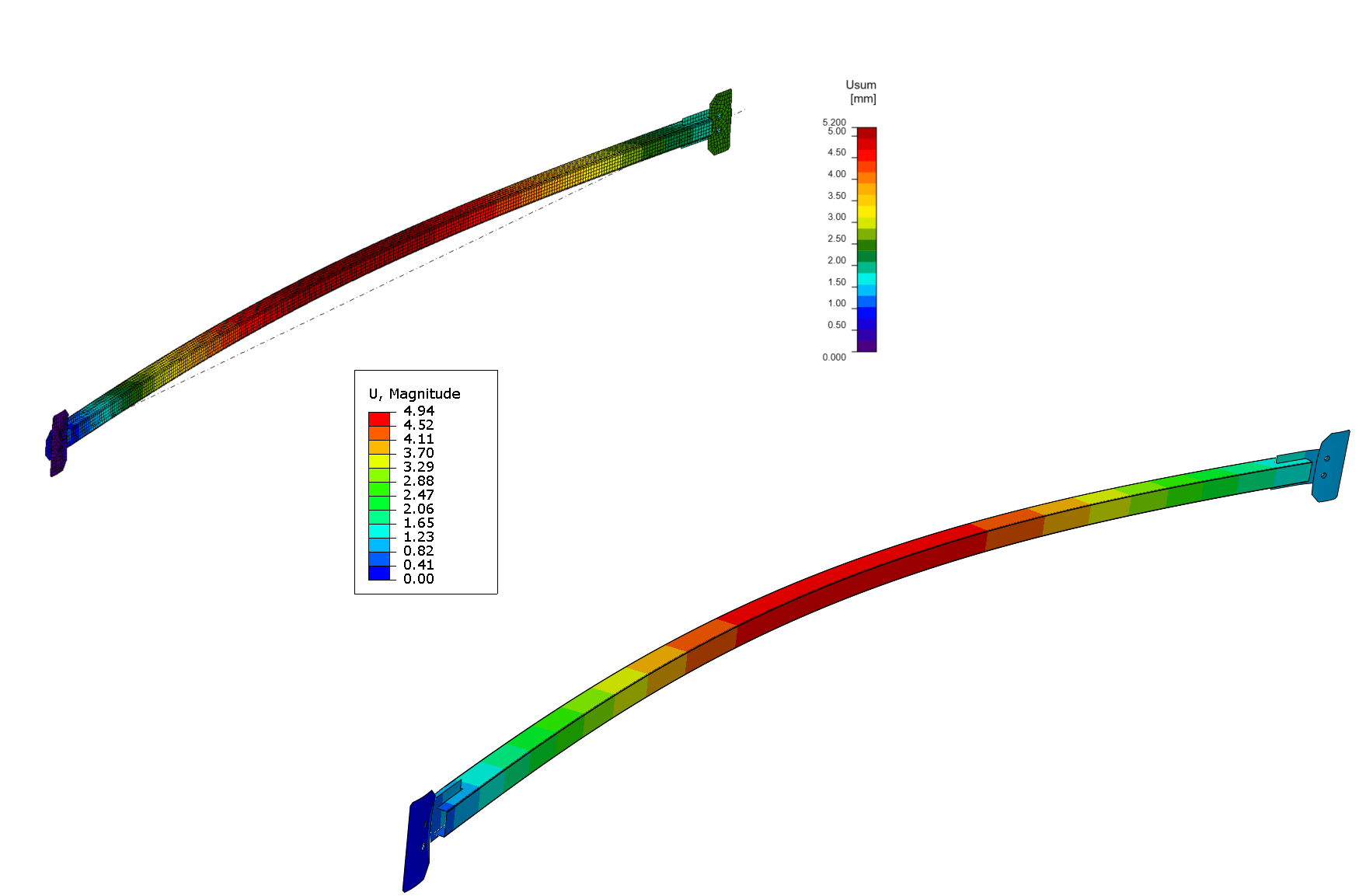
07) IDEA StatiCa total deformation(left), ABAQUS total deformation(right)
The material’s response is elastic since the stresses impact only the local area around the opening’s yield point. This localized effect suggests that the material doesn’t undergo permanent deformation. Additionally, the deflections in both models show an excellent match, indicating consistent and reliable results.
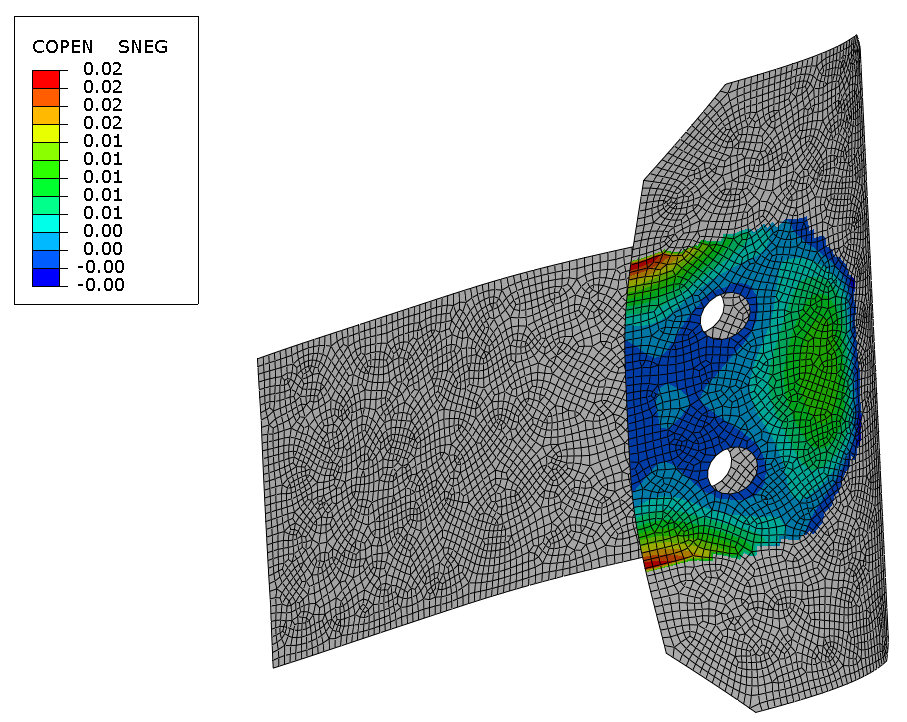
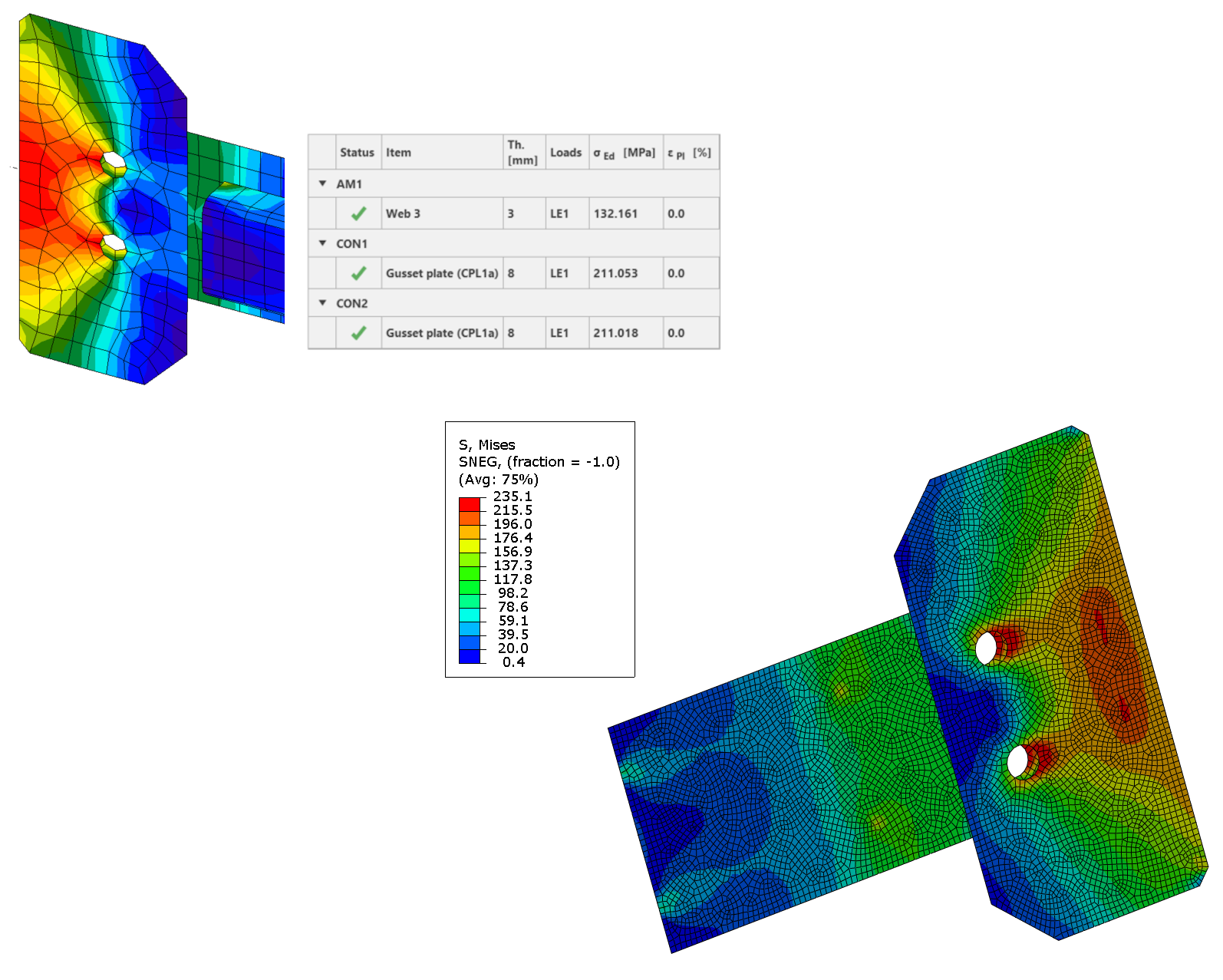
05) IDEA StatiCa equivalent stress(left), ABAQUS equivalent stress(right)
Opening in the contact –
ABAQUS provides an additional output called “COPEN”, which provides information about the gap or opening between two plate.
Linear buckling analysis
Linear buckling analysis is a computational technique that helps predict when and how structures like columns, beams, and shells might buckle under certain loads. It’s all about finding that critical point – the load or load factor – where the structure stops being stable and starts to buckle. This kind of analysis is super important for engineers to make sure their designs are safe and can stand up to the loads they’ll face without losing stability.
08) Linear vs. nonlinear buckling
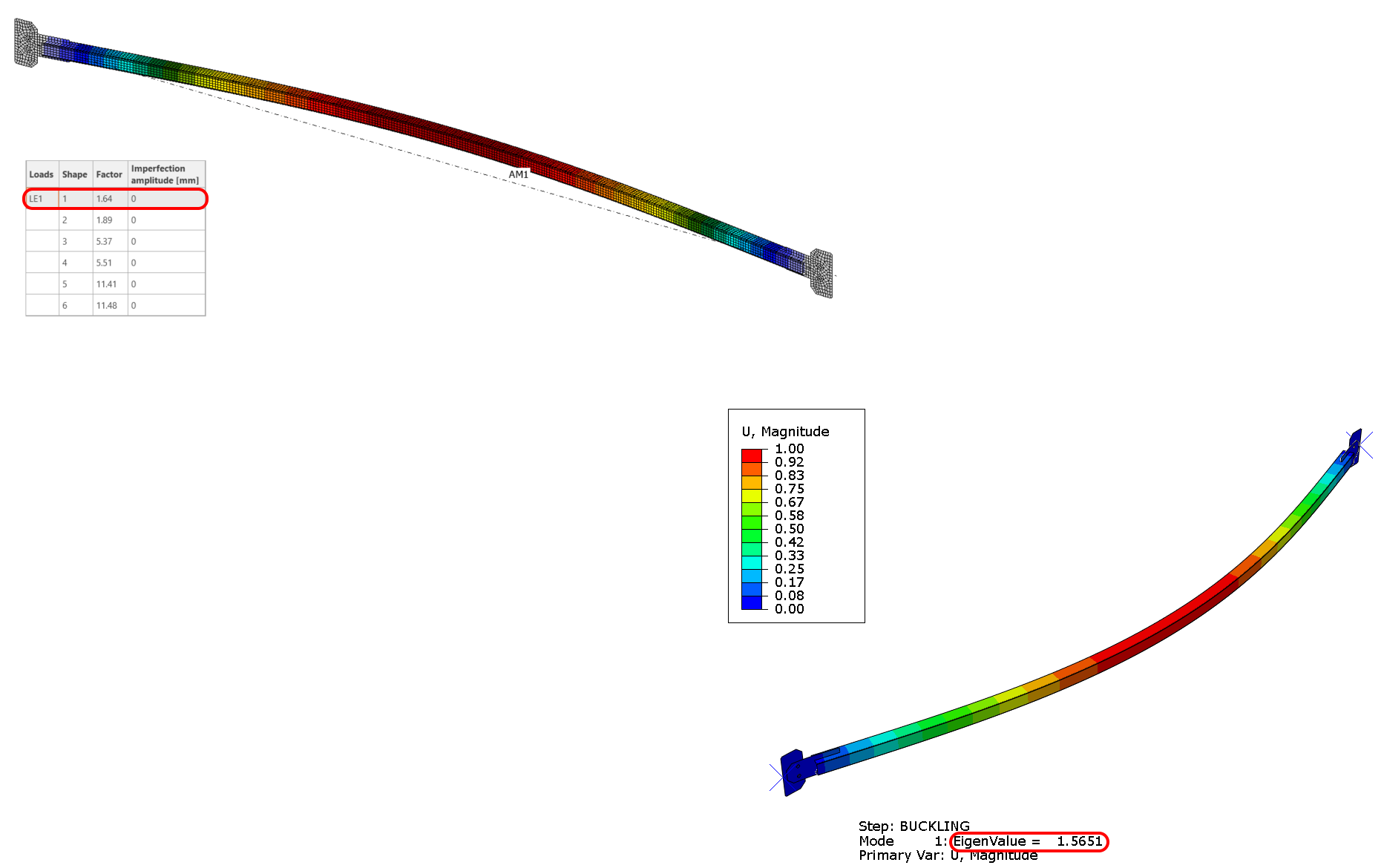
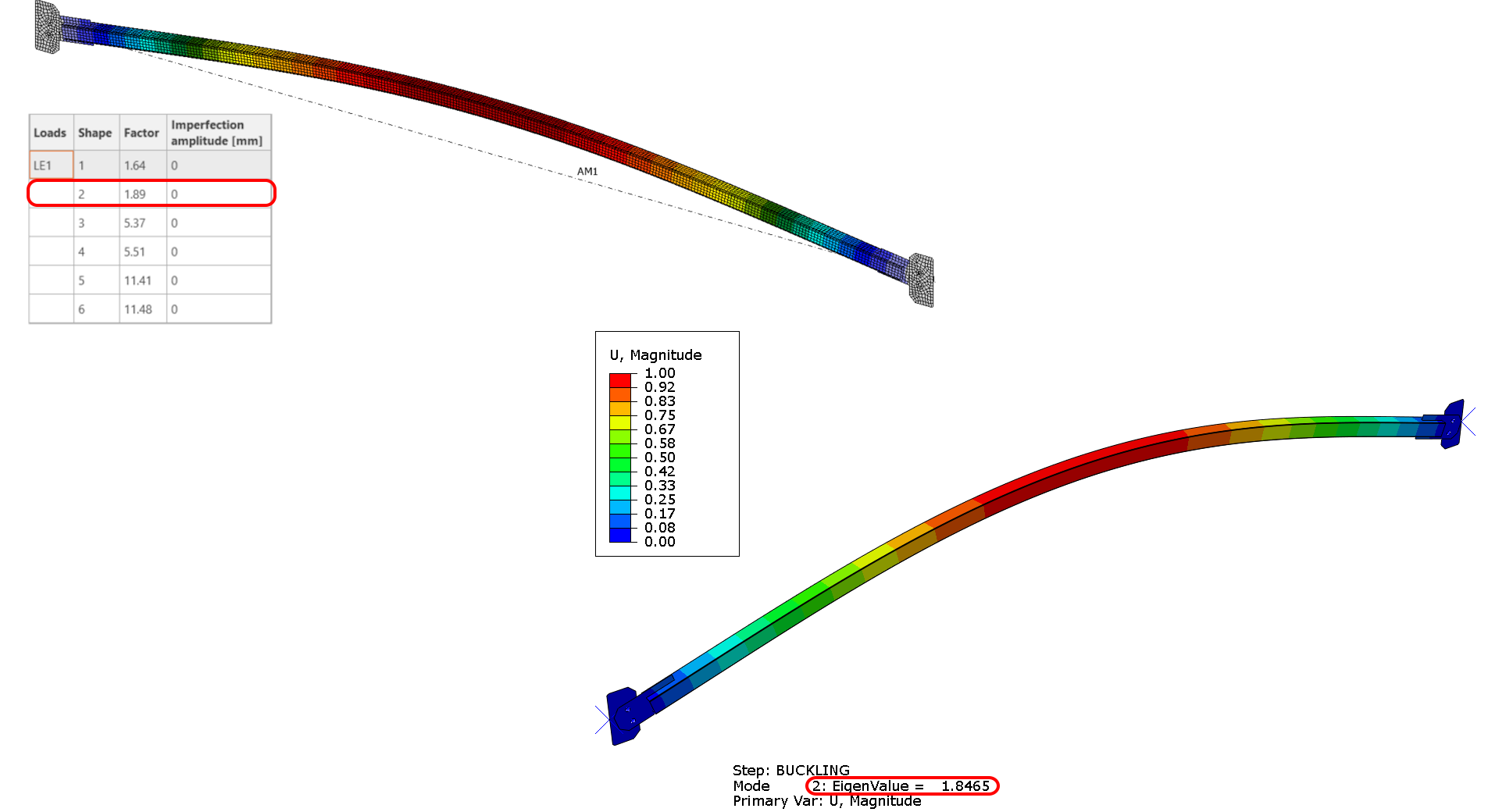
Linear buckling analysis significantly aids in predicting structural failures by generating eigenmodes and critical load factors. Verification shows a close match between IDEA Statica and ABAQUS, with minimal error. The first buckling mode’s critical factor was 1.64 in IDEA Statica, closely aligned with 1.57 in ABAQUS.
09) IDEA StatiCa first buckling shape(left), ABAQUS first buckling shape(right)
10) IDEA StatiCa second buckling shape(left), ABAQUS second buckling shape(right)
Imperfection
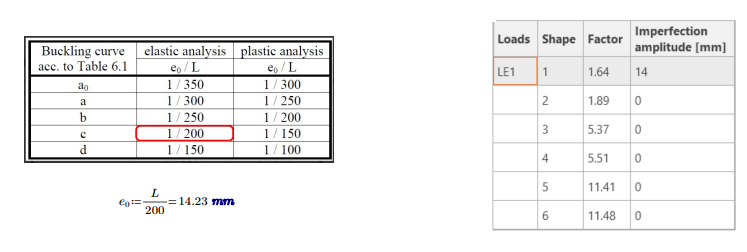
11) Imperfection values
Following the EN 1993-1-1 standards, incorporating imperfections is essential for accurate analysis for the HESCO project. The size of these local imperfections depends on the buckling curve specified in Table 6.1 and the section’s classification. For the SHS 50/50/3, which falls under buckling curve C, the relevant local imperfection to consider is 14 mm.
Geometrical and material nonlinear analysis with imperfection
Geometrical and Material Nonlinear Analysis (GMNIA) is a crucial engineering tool for studying how structures behave under extreme loads. It accounts for geometric nonlinearity (shape changes), material nonlinearity (changes in material properties), and any pre-existing imperfections or deformations. This comprehensive approach allows engineers to better predict a structure’s response to loading, aiding in informed design and safety decisions for the HESCO porject.
The analysis method seeks equilibrium at every step, starting with the initial deformed shape from Linear Bifurcation Analysis’s (LBA) imperfection. If equilibrium isn’t achieved, the analysis halts.
Key aspects include:
– Material Nonlinearity: This occurs when materials move beyond elastic deformation into plastic yielding, altering their behavior.
– Stability Issues: These emerge when the structure can’t complete further iterations due to equilibrium loss or reaching a bifurcation point.
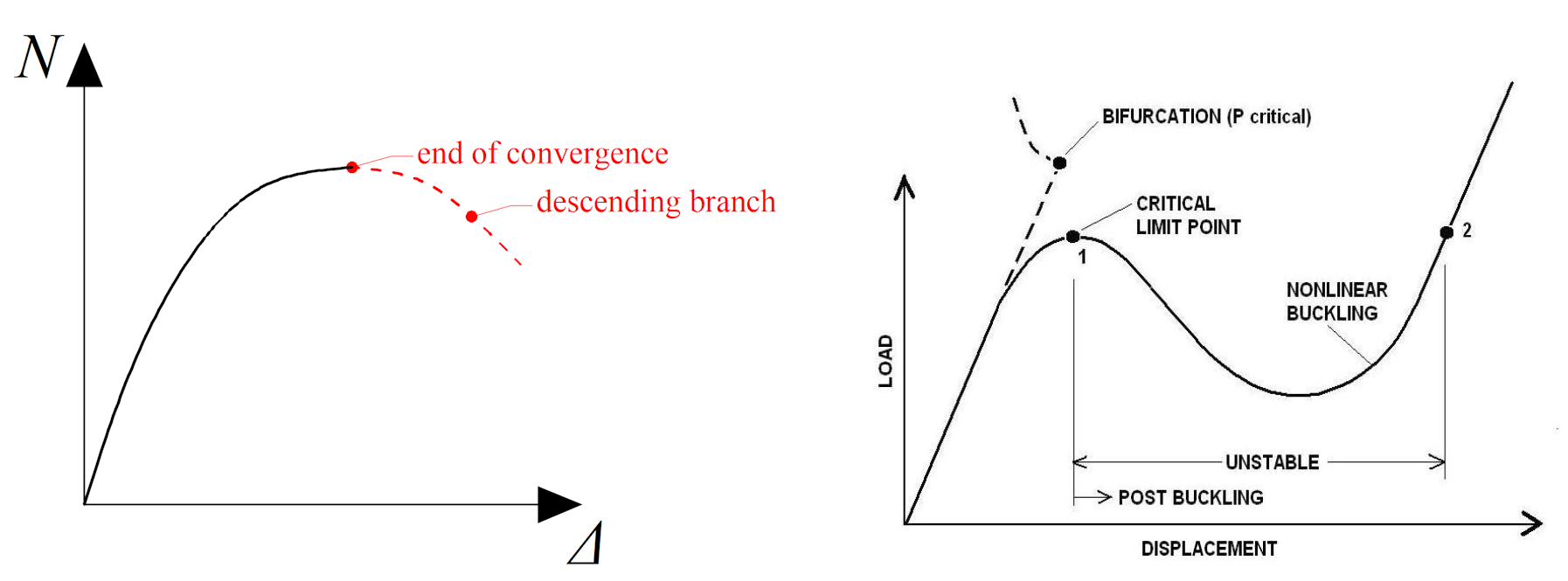
IDEA StatiCa employs the Newton-Rhapson method for solving equilibrium for the HESCO project. The analysis concludes at the peak point, without resolving the descending branch. This approach aligns with structural engineers’ focus on stable solutions, as unstable conditions are generally outside their primary scope of concern.
IDEA StatiCa Solution to the Imperfection
For the Geometrical and Material Nonlinear Analysis (GMNIA), the starting point is the shape obtained from the buckling analysis. In our scenario, this initial shape resembles a half-sinusoidal wave.
Regarding equivalent stress, we’ve observed a considerable increase in stress levels, nearing the yield point. This suggests that some components are close to yielding. As a result, the IDEA StatiCa model is now in a state where plastic deformation is likely to occur.
12) Load deformation curve IDEA StatiCa (left), ABAQUS(right)
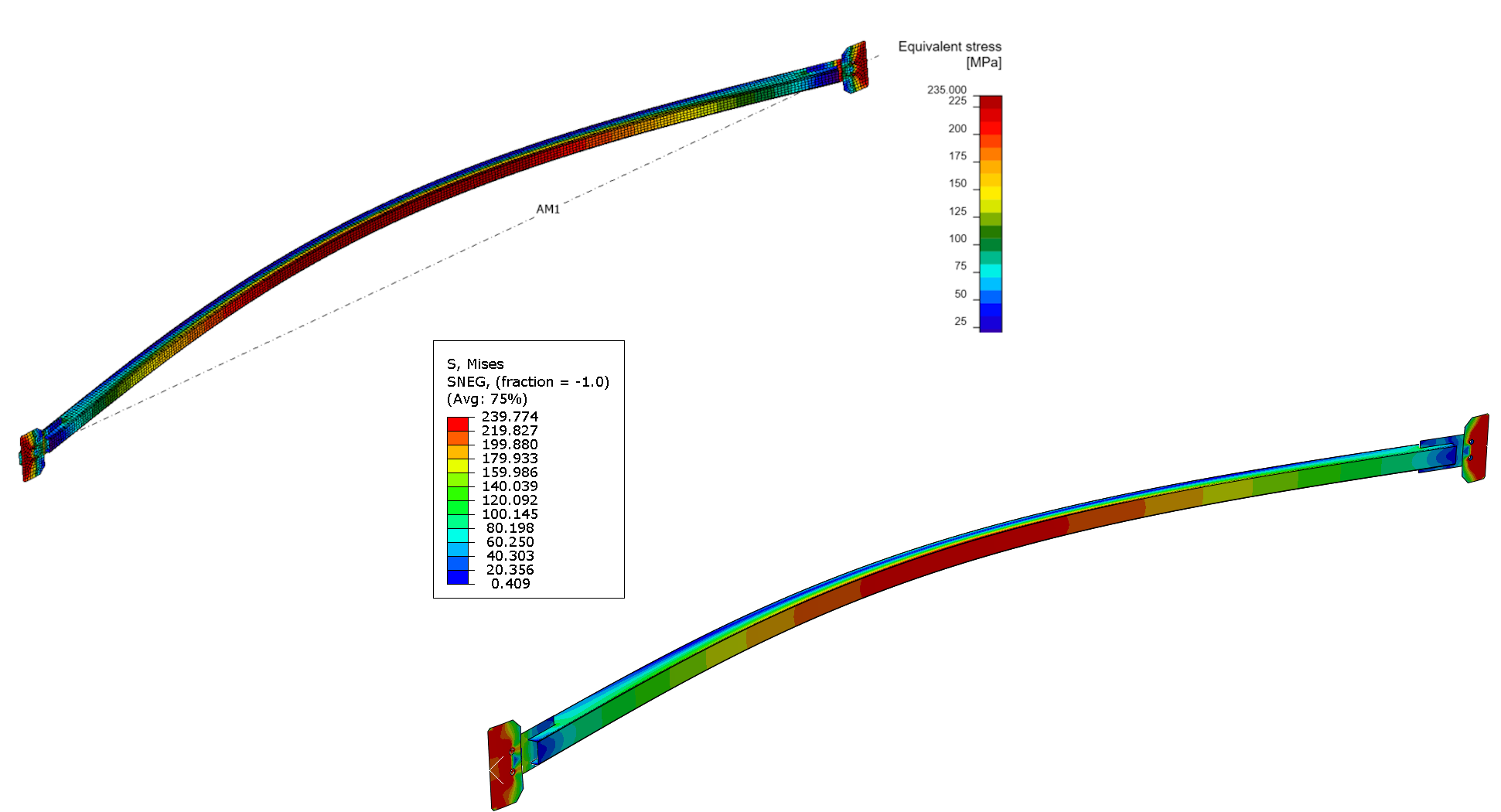
13) IDEA StatiCa equivalent stress(left), ABAQUS equivalent stress(right)
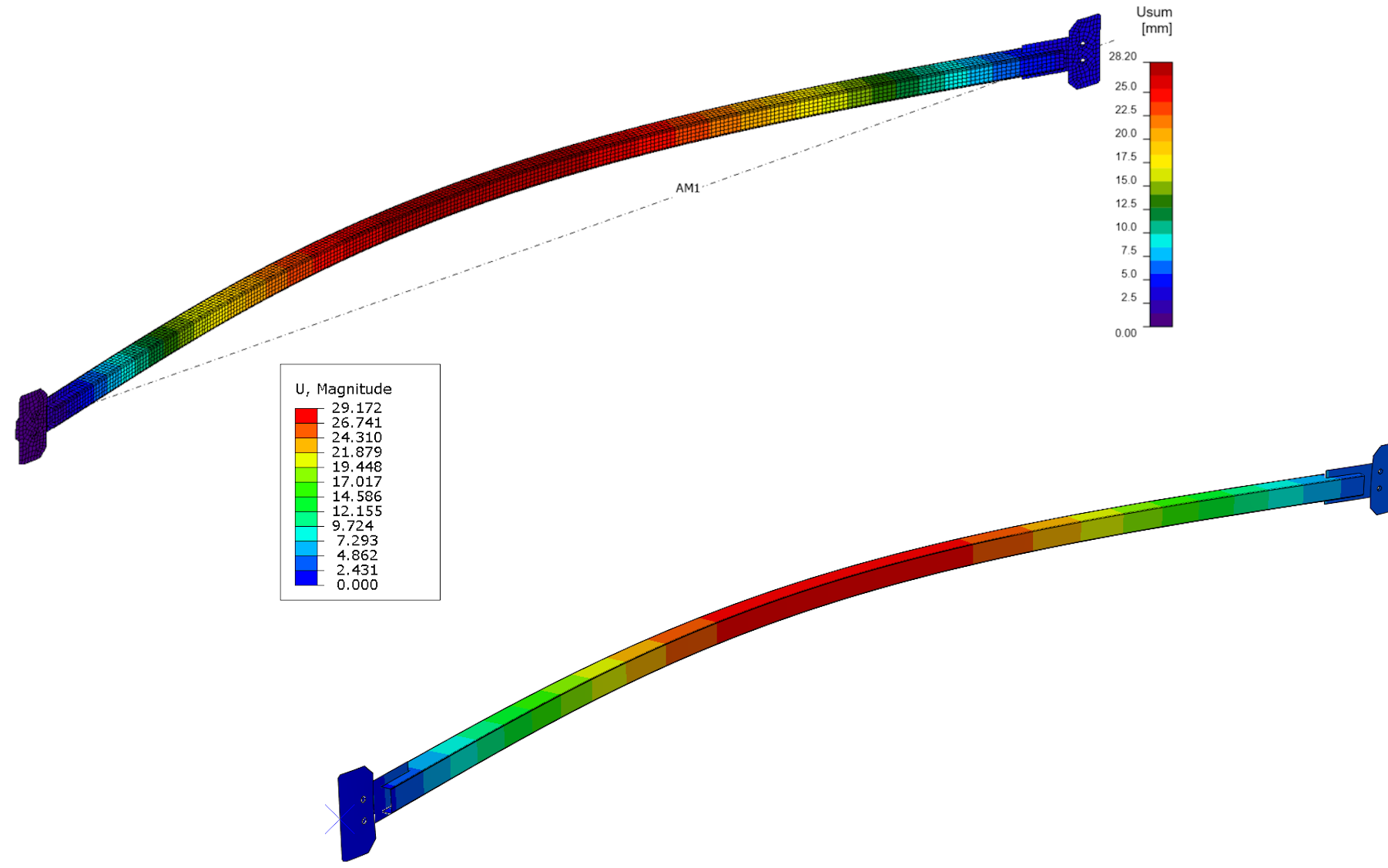
Plastic strain and plastic regions
Yielding has started to occur at the connection points and in the middle of the bracing in our analysis.
Force-deformation graph
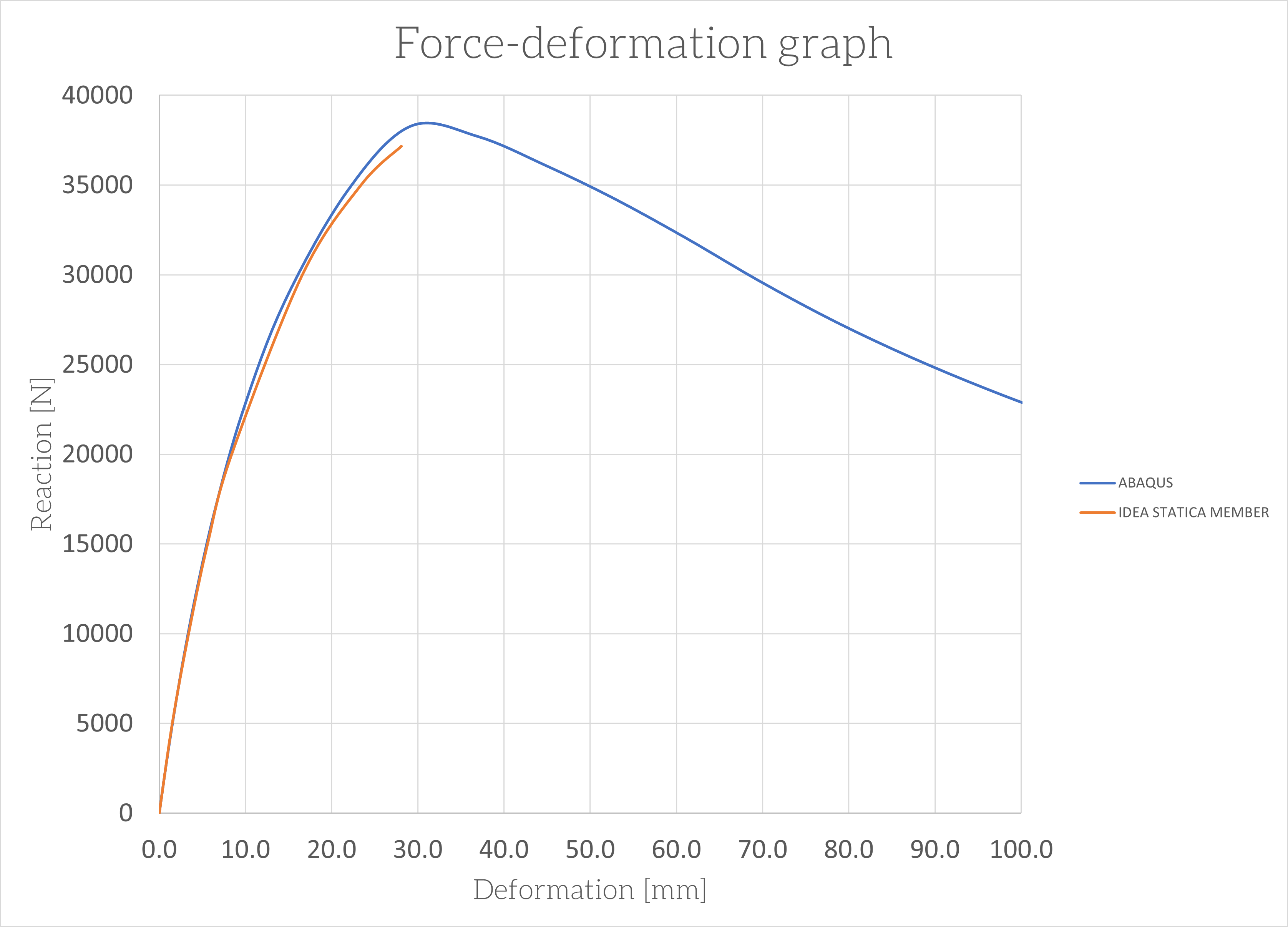
Conclusion
The verification process for IDEA StatiCa Member was centered on demonstrating its effectiveness in ensuring safe and compliant design for a range of structures. Rigorous testing and evaluation were carried out to assess its accuracy and adherence to industry standards. The aim was to thoroughly understand its features and benefits, particularly in streamlining the design process and reducing errors.
Comparing the results from IDEA StatiCa Member with analytical solutions and ABAQUS revealed a high degree of accuracy, with a 95% match. The maximum design value was identified as 35.8 kN. Using IDEA StatiCa Member, this increased to 37.1 kN, and ABAQUS further showed a peak value of 38.2 kN, highlighting the precision of these methods.
The consistent results across equivalent stress, plasticity, and deformations in various applications underscore the reliability of the code evaluation. This consistency confirms the code’s robustness and accuracy in predicting system responses, making it a reliable tool for both professional and academic settings.
Try IDEA StatiCa for Free

Steel Pins Design with IDEA StatiCa
Using pins in IDEA Connection Pins are commonly used in various steel structures, typically for linking bracing, diagonal, rod and bar elements, or other structural elements that transfer tension and compression forces. This type of connector is now available in

NEW IDEA STATICA 24.0 IS HERE WITH SOME GROUNDBREAKING TOOLS AND FEATURES!
NEW IDEA STATICA 24.0 IS HERE WITH SOME GROUNDBREAKING TOOLS AND FEATURES! IDEA StatiCa 24.0 marks two big anniversaries of our CBFEM method and Connection application – a decade of making the right connections for your structures!! We are also
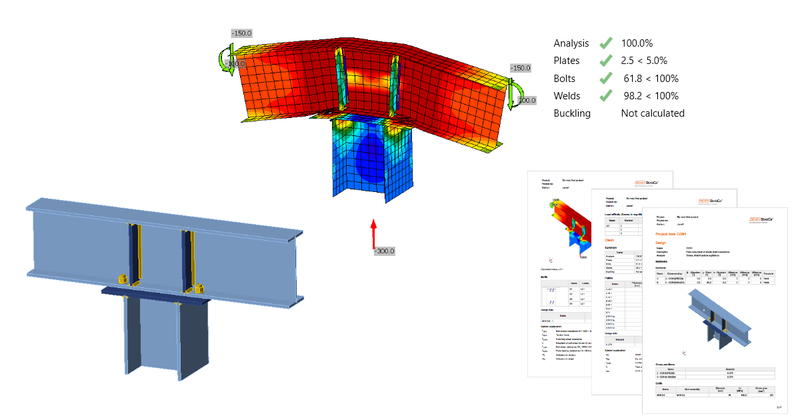
Beam to Column Connection Design: IDEA StatiCa In-depth Guide
Beam to Column Connection Design: IDEA StatiCa In-depth Guide This is a tutorial that utilises IDEA StatiCa Connection to promptly design and code-check steel connections. Through this article, we will illustrate how to model a simple steel connection, and also

Stability of slender concrete columns
How do you ensure the stability of slender concrete columns, while maintaining both economic feasibility and safety in the design? This article explains how IDEA StatiCa Member empowers designers to maximize the potential of their reinforced concrete structures through a streamlined and efficient workflow.
Advanced Topics in IDEA StatiCa Detail Loading
Advanced Topics in IDEA StatiCa Detail Loading Inputting loads in your project is seen as the foundation of any project. The article covers topics, such as the correct specification of load from the shearing connection, partial factors or load under
Construction Computing Features IDEA StatiCa
Over the years, IDEA StatiCa has established its name as a prominent figure across the field of structural engineering, especially when it comes to steel connection design. Construction Computing Magazine As a result, we have been getting more attention from